
Of course in reality there is that 3rd dimension, but it isn't important for the math. Just like the math for a 2-D object like a circle or square can be used to predict very accurately the behavior of a true 3-D object like a circle or square cut out of sheet metal.
Sure, mathematically, a line is only 1 dimensional, but the math of that 1 dimensional object can be used to predict with incredible accuracy the behavior of a true 3 dimensional object such as a rope or chain. For a long thin rod or chain, it is perfectly reasonable to define a mass per unit length - and is done so often to predict the shape a hanging chain or rope will take. In the sheet metal example above, it is perfectly reasonable to define a mass per unit area.
#Moment of inertia of a circle full
Note that the height, h isn't even part of the equation! That means that it doesn't matter if the height is 1 cm, 1 million cm, or even infinite or zero centimeters! The answer is the same!Įven further proving my point is that the formula for the cuboid and the formula for the "thin rectangular plane" are the same! The depth doesn't matter at all! You don't even have to perform the 3-D calculations to get the same answer as the 2-D ones, meaning that you don't have to do the extra work of the full 3-D calculation.Īnd, the fact is, you can define densities not just as mass per unit volume.

I_z = \frac where I_z is the MOI about the axis, m is the mass of the cylinder, and r is the radius. Specifically, the one for a solid cylinder: Let's even look at your list of moments of inertia. Sure, technically, that is a very squat cylinder or a parallelepiped with a very thin depth, but if you use an MOI calculation for a 2-D object with a given mass per unit area, the answer between the 3-D and the 2-D calculations will be negligibly different - implying that the 2-D approximation is very, very good. Consider if I made a square and a circle out of very thin sheet metal. Genralz, in case you mean MOI of a cylinder or cubiod etc.īut I'm not just "making up a mass that has no meaning". Yes you can make up an mass that has no meaning, I don't care. The simple fact is that the MOI formula requires a mass to have some meaning. To a very large extent, it doesn't really matter at all that no 2-D object has mass, or that there is no such thing as a perfect circle, mathematically such objects do exists and we can perform mathematics on them.įrom what I read genralz isn't interested in math for the math. It is a simplifying assumption made primarily to make the math easier and get a result that is going to be very close to the real world. Just like mathematically we can and do use point masses and point charges all the time, despite there being no such thing in the real world. Mathematically we can assign an area density or mass per unit area and make it mathematically have mass. If you want to start down that road, why not just say that a circle or square can't have an MOI because there is no such thing as a perfect circle or perfect square? Moment of inertia along the third axis i.e Z axis is calculated by- Izz = Ixx+ Iyy.Kedas, while physically being merely a 2-D object a circle or square wouldn't have any mass in the real world, it doesn't prevent us from mathematically talking about a circle or square's MOI. As we know moment of inertia is always along some axis that's why these are the moment of inertia along the two axis. Iyy is the moment of inertia along the y axis. Ixx is the moment of inertia along the x axis. The 2 nd moment of area, or second area moment and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. Moreover, what is meant by second moment of area? If the function represents physical density, then the zeroth moment is the total mass, the first moment divided by the total mass is the center of mass, and the second moment is the rotational inertia. First moment of area is useful when calculating area distribution, symmetry and shear flow.īeside above, what is first moment and second moment? In mathematics, a moment is a specific quantitative measure of the shape of a function. Second moment of area is resistance to twisting due to applied torque. Moment of Inertia or Mass moment of inertia is resistance to angular deflection due to applied torque. In respect to this, what is the difference between moment of inertia and second moment of area? Both beams have the same area and even the same shape. The second moment of area is a measure of the 'efficiency' of a cross-sectional shape to resist bending caused by loading.
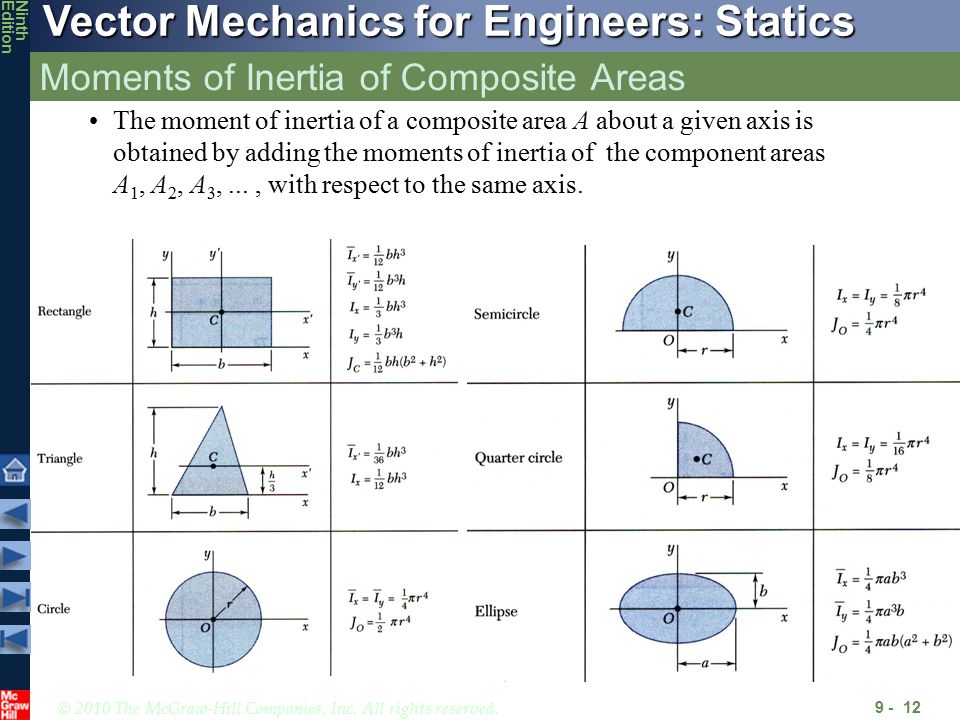
The second moment of area is also known as the moment of inertia of a shape.


 0 kommentar(er)
0 kommentar(er)
